반응형
17. 무한장 직선 전하로부터 수직거리 p[m]되는 점에서 전계의 세기는?
① p에 반비례 ② p에 비례
③ p2에 비례 ④ p2에 반비례
• 설명
- 두 가지 방법으로 구할 수 있다.
- ① 쿨롱의 법칙, ② 가우스 법칙
- 풀이 ①에서는 직각좌표계를 사용하였다.
- 풀이 ②에서는 원통좌표계를 사용하였다.
- 풀이 ①의 계산에 활용된 적분 공식 참고하자

답은 ①
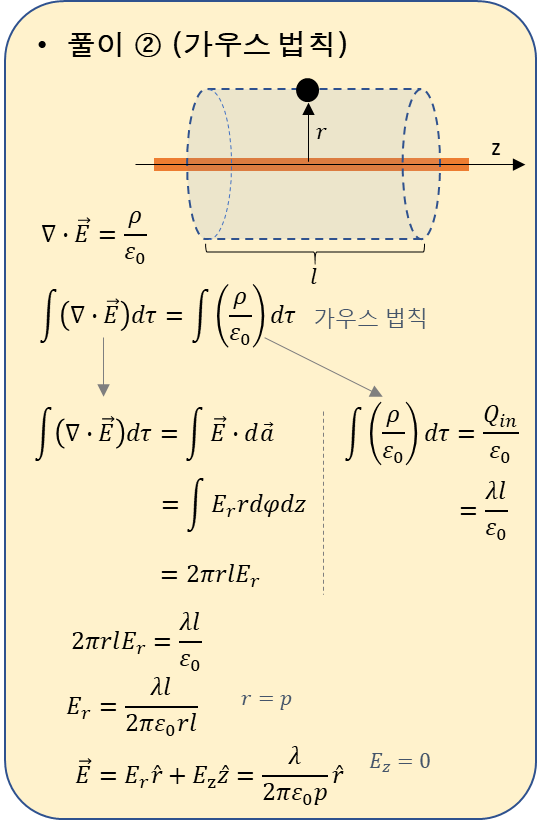

개인적으로 푼 거라서 틀릴 가능성 있습니다.
혹시 틀린 부분 있으면 댓글요~
도움이 되었다면 ♡ 클릭요~
♡ 클릭 안 하면, 시험에서 떨어짐
반응형
'전기산업기사(20100307) - 전기자기학' 카테고리의 다른 글
| 15. 평형상태에서 도체의 전하분포와 전계에 관한 성질로 옳지 않은 것은? (0) | 2023.09.02 |
|---|---|
| 16. v[m/s]의 속도로 전자가 B[Wb/m2]의 평등 자계에 직각으로 들어가면 원운동을 한다. 이때이 각속도 ω[rad/s]와 주기 T[sec]에 해당되는 것은? (2) | 2023.09.02 |
| 18. 등전위면에 대한 설명으로 옳은 것은? (0) | 2023.09.02 |
| 19. 무한길이의 직선 도체에 전하가 균일하게 분포되어 있다. 이 직선 도체로부터 l[m]거리에 있는 점의 전계의 세기는? (0) | 2023.09.01 |
| 20. 진공 중에서 8π[Wb]의 자하로부터 발산되는 총 자력선의 수는? (0) | 2023.08.30 |



